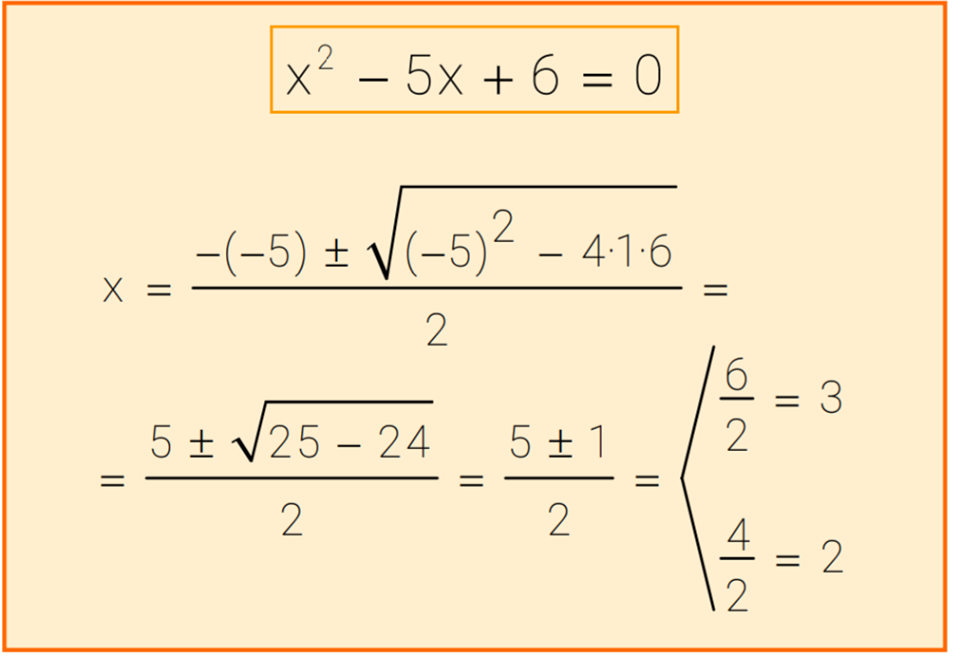Have you ever wondered how mathematicians model the trajectory of a basketball or the arc of a bridge? The answer lies in the fascinating world of quadratic equations. These mathematical expressions, also known as second-degree polynomial equations, play a crucial role in various fields, from physics and engineering to economics and computer science.
Quadratic equations are characterized by their highest power of the variable being two. They take the general form of ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'x' represents the unknown variable. These equations often yield two solutions, known as roots, which can be real or complex numbers.
The history of quadratic equations can be traced back to ancient civilizations like the Babylonians, Egyptians, and Greeks. These civilizations developed ingenious methods for solving specific types of quadratic equations, often motivated by practical problems related to land measurement, construction, and astronomy. Over centuries, mathematicians like Brahmagupta, al-Khwarizmi, and François Viète made significant contributions, leading to the development of the quadratic formula—a general solution for any quadratic equation.
The importance of quadratic equations extends far beyond the realm of theoretical mathematics. They serve as powerful tools for modeling and solving real-world problems. For instance, physicists use them to describe projectile motion, engineers rely on them to design parabolic structures, and economists employ them to analyze market trends.
One of the main issues related to quadratic equations is the possibility of encountering complex roots. While real roots have straightforward interpretations, complex roots can pose challenges in certain applications. However, mathematicians and scientists have developed methods to handle and interpret complex roots, expanding the applicability of quadratic equations even further.
Advantages and Disadvantages of Quadratic Equations
| Advantages | Disadvantages |
|---|---|
| Versatile and applicable to various fields. | Can have complex solutions, which might not always have direct physical interpretations. |
| Relatively simple to solve using the quadratic formula or factoring. | May not accurately represent highly complex real-world phenomena that require higher-order equations. |
| Provide a foundation for understanding more advanced mathematical concepts. |
In conclusion, quadratic equations, despite their seemingly abstract nature, hold immense significance in our understanding and interaction with the world around us. From modeling physical phenomena to solving practical problems, their applications are vast and continue to expand with ongoing research and technological advancements. Learning about quadratic equations opens doors to a deeper appreciation for the power and elegance of mathematics in explaining and shaping our universe.
Long hair dont care rocking fringe over 50
Crafting a digital first impression discord server icon size recommendations
Myths unearthed a look at mythical creatures list and descriptions
ecuaciones de 2 grado que son - You're The Only One I've Told
ecuaciones de 2 grado que son - You're The Only One I've Told
ecuaciones de 2 grado que son - You're The Only One I've Told
ecuaciones de 2 grado que son - You're The Only One I've Told
ecuaciones de 2 grado que son - You're The Only One I've Told
ecuaciones de 2 grado que son - You're The Only One I've Told
ecuaciones de 2 grado que son - You're The Only One I've Told
ecuaciones de 2 grado que son - You're The Only One I've Told
ecuaciones de 2 grado que son - You're The Only One I've Told
ecuaciones de 2 grado que son - You're The Only One I've Told
Arriba 85+ imagen modelo grafico ejemplos - You're The Only One I've Told
ecuaciones de 2 grado que son - You're The Only One I've Told
ecuaciones de 2 grado que son - You're The Only One I've Told
ecuaciones de 2 grado que son - You're The Only One I've Told
ecuaciones de 2 grado que son - You're The Only One I've Told