Have you ever looked at a tall building and wondered how its height is measured? Or perhaps marveled at the complexity of architectural designs, especially curved structures? The answers often lie in a fascinating branch of mathematics: trigonometry. While many associate it with textbook exercises, trigonometry extends its reach far beyond the classroom, playing a crucial role in numerous real-world applications.
Trigonometry, at its core, deals with the relationships between angles and the ratios of sides in triangles. Its origins can be traced back to ancient civilizations like the Egyptians and Babylonians, who used it for land surveying and astronomy. The word itself is derived from Greek words meaning "triangle" and "measure." Over centuries, mathematicians developed trigonometric functions and identities, forming the foundation for this field. This evolution has been instrumental in shaping various disciplines.
The significance of understanding angles and distances transcends theoretical boundaries. Architects, for instance, rely heavily on trigonometry to calculate precise dimensions, ensuring structural stability and aesthetically pleasing designs. Similarly, engineers utilize these principles to construct bridges, roads, and other marvels of engineering. The ability to model and predict the behavior of objects in motion, from projectiles to sound waves, hinges on the application of trigonometric functions.
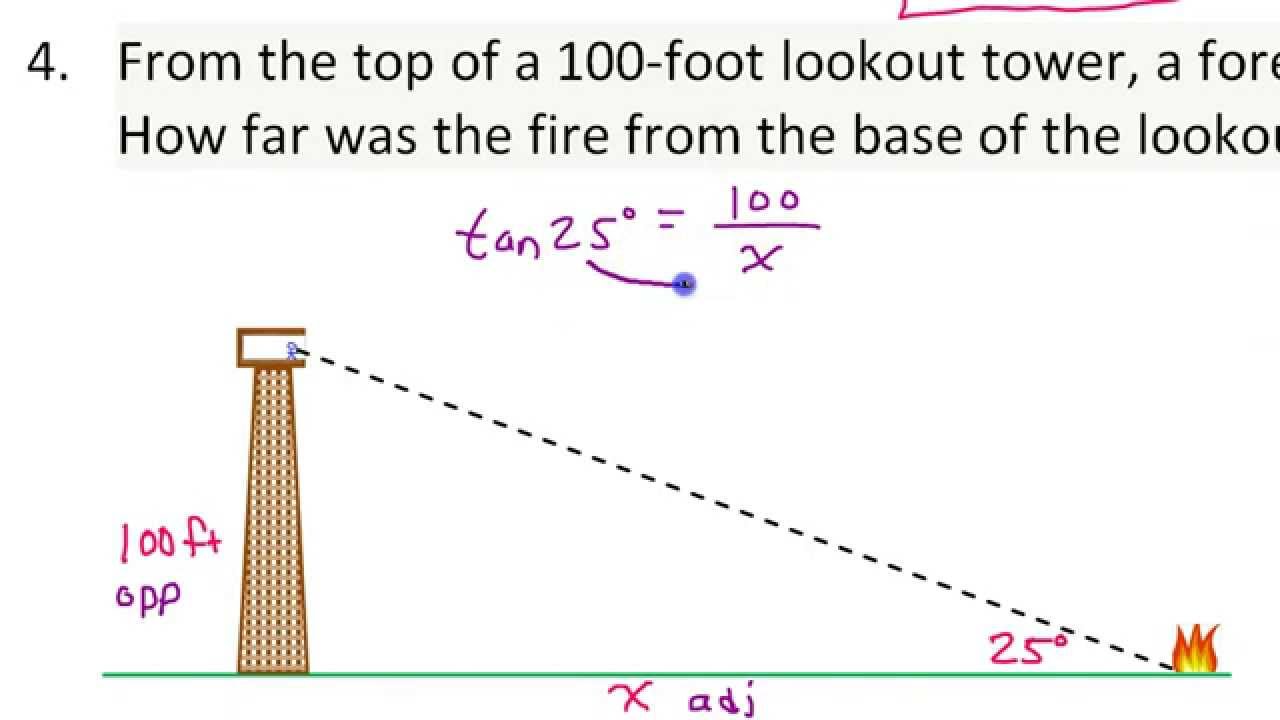
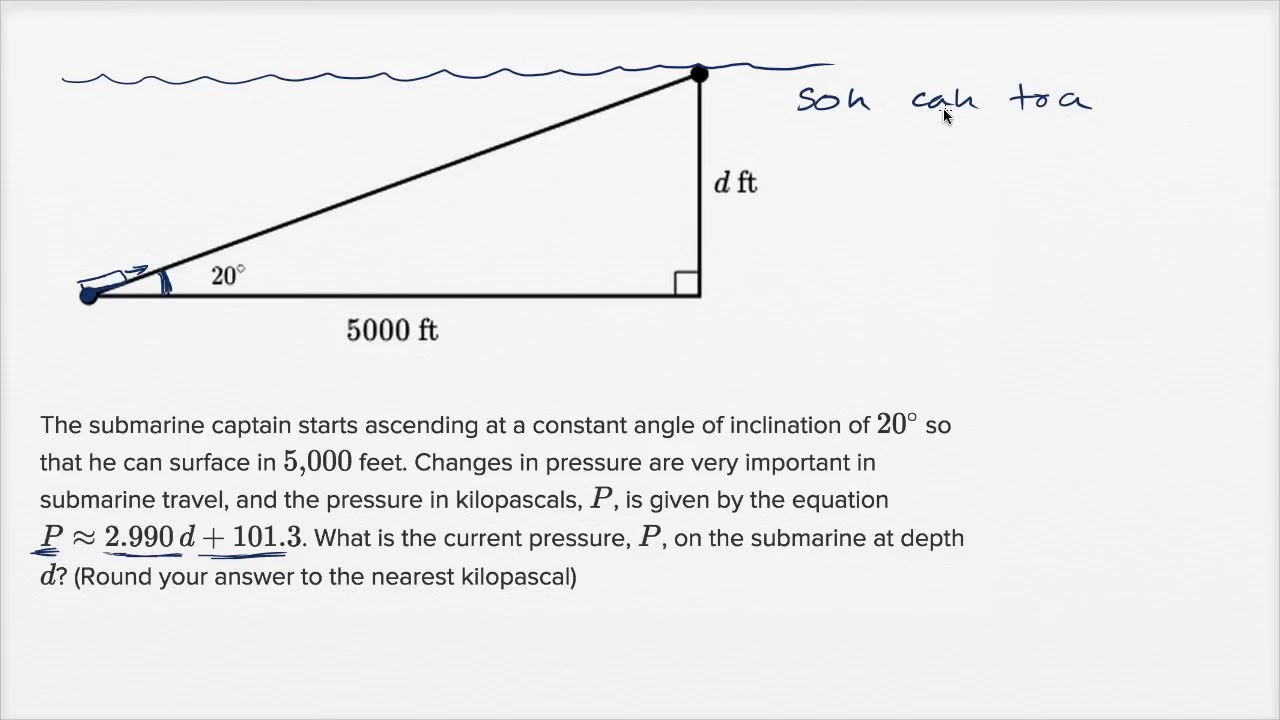
Consider a simple example. Imagine you need to determine the height of a tree. By measuring the distance from the tree and the angle of elevation to its top using a simple tool like a clinometer, you can employ trigonometric ratios to calculate its height. This basic principle finds applications in various fields, from navigation, where sailors use it to chart courses, to astronomy, where astronomers use it to determine distances to celestial objects.
One of the key strengths of trigonometry lies in its ability to simplify complex problems by breaking them down into solvable triangles. Let's take the example of a surveyor mapping out a piece of land with irregular boundaries. Using triangulation, they can divide the area into multiple triangles, measure the angles and sides of each triangle, and accurately calculate the total area of the land. This method is not only efficient but also highly precise, demonstrating the practical value of trigonometry in real-world scenarios.
Advantages and Disadvantages of Using Trigonometry for Real-World Applications
| Advantages | Disadvantages |
|---|---|
| Provides accurate measurements and calculations. | Can be complex and time-consuming for intricate problems. |
| Versatile applications in various fields. | Requires precise measurements and data for accurate results. |
| Simplifies complex problems by breaking them down into manageable parts. | May involve the use of specialized tools and software. |
While trigonometry offers numerous benefits, it's essential to acknowledge its limitations. Applying trigonometric principles in real-world situations often requires accurate measurements and data. Inaccurate or incomplete data can lead to erroneous results, highlighting the importance of precision. Furthermore, as the complexity of the problem increases, so does the mathematical computation involved. This often necessitates the use of specialized software or calculators, potentially posing a challenge in resource-limited settings.
In conclusion, trigonometry, often perceived as a purely academic subject, plays a surprisingly significant role in our everyday lives. Its applications extend far beyond textbooks, influencing fields as diverse as architecture, engineering, navigation, and many more. From calculating the height of a building to charting the course of a ship, trigonometry provides the tools to understand and navigate the world around us. While challenges like data accuracy and computational complexity exist, the benefits of using trigonometry to solve real-world problems far outweigh the obstacles, making it an invaluable tool in our quest to understand and shape the world we live in. Embrace the power of triangles and unlock a deeper understanding of the world around you!
Unlocking the power of the instagram logo outline svg
Navigating arkansas medical marijuana your guide to the adh mmj program
Access granted your guide to xenia ohio municipal court public access
trigonometry exercises real word application - You're The Only One I've Told
trigonometry exercises real word application - You're The Only One I've Told
Solving Trigonometric Equations Worksheets - You're The Only One I've Told
trigonometry exercises real word application - You're The Only One I've Told
trigonometry exercises real word application - You're The Only One I've Told
trigonometry exercises real word application - You're The Only One I've Told
trigonometry exercises real word application - You're The Only One I've Told
trigonometry exercises real word application - You're The Only One I've Told
trigonometry exercises real word application - You're The Only One I've Told
trigonometry exercises real word application - You're The Only One I've Told
trigonometry exercises real word application - You're The Only One I've Told
trigonometry exercises real word application - You're The Only One I've Told
ideas and resources for mathematics teachers of 10 to 16 year olds - You're The Only One I've Told
trigonometry exercises real word application - You're The Only One I've Told
trigonometry exercises real word application - You're The Only One I've Told