Pernahkah anda melihat formula matematik yang panjang dan berselirat, penuh dengan simbol-simbol aneh yang membuatkan kepala anda pening? Jangan risau, anda tidak keseorangan! Tanda-tanda dalam rumus matematik boleh menjadi seperti bahasa rahsia, tetapi dengan sedikit pengetahuan, anda boleh menguasainya dan membuka kunci kepada dunia matematik yang menakjubkan.
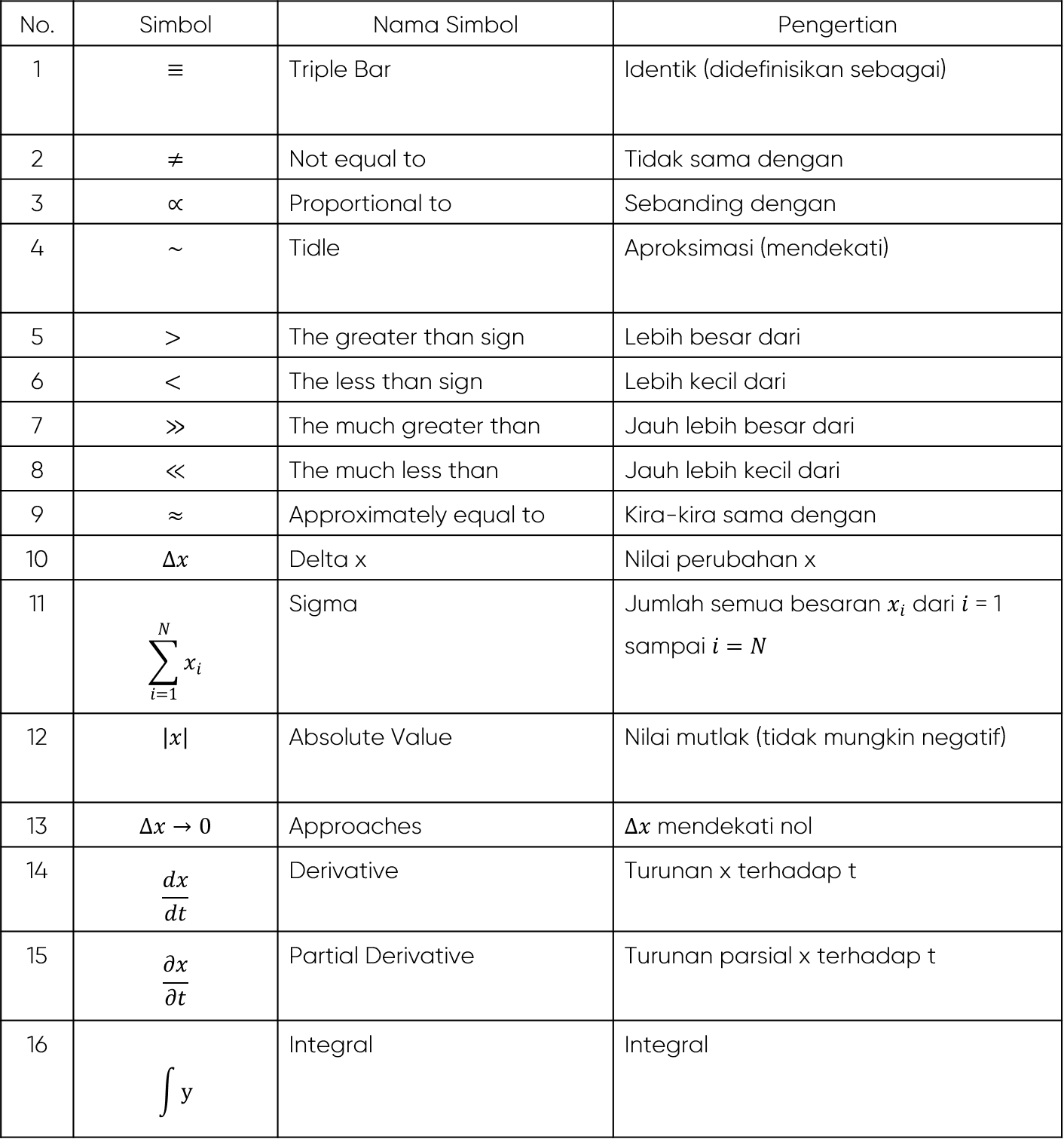
Tanda-tanda dalam rumus matematik memainkan peranan penting dalam menyampaikan maklumat dengan tepat dan ringkas. Ia seperti kata-kata dalam ayat, yang disusun dengan teliti untuk mencipta makna. Daripada simbol asas seperti tambah (+) dan tolak (-) hingga kepada konsep yang lebih kompleks seperti kamiran (∫) dan pembezaan (d/dx), setiap tanda mempunyai makna dan fungsi tertentu.
Sejarah tanda matematik bermula sejak zaman purba, dengan tamadun seperti Babilon dan Mesir menggunakan simbol untuk mewakili nombor dan operasi. Sistem simbol ini berkembang dari masa ke masa, dengan sumbangan daripada cendekiawan Yunani, India, dan Arab. Pada abad ke-17, ahli matematik seperti René Descartes dan Gottfried Wilhelm Leibniz memperkenalkan sistem notasi moden yang kita gunakan hari ini.
Kepentingan tanda matematik tidak boleh dipertikaikan. Ia membolehkan ahli matematik untuk berkomunikasi idea-idea mereka dengan tepat dan berkesan, tanpa mengira bahasa atau budaya. Ia juga membolehkan kita untuk menyelesaikan masalah yang kompleks, membuat ramalan, dan memajukan pemahaman kita tentang dunia.
Namun, salah faham dan penggunaan tanda matematik yang salah boleh menyebabkan kesilapan dan salah tafsiran. Oleh itu, adalah penting untuk memahami makna dan fungsi setiap tanda, serta konvensyen dan peraturan yang mengawal penggunaannya.
Kelebihan dan Kekurangan Tanda Matematik
Tanda matematik menawarkan beberapa kelebihan, tetapi ia juga mempunyai beberapa kekurangan. Berikut adalah jadual yang meringkaskan beberapa perkara penting:
| Kelebihan | Kekurangan |
|---|---|
| Ketepatan dan kejelasan | Kekeliruan dan kerumitan |
| Kecekapan dan keringkasan | Keperluan untuk pembelajaran dan amalan |
| Komunikasi universal | Abstraksi dan ketidaksesuaian dengan konteks dunia sebenar |
Amalan Terbaik untuk Melaksanakan Tanda Matematik
Berikut adalah beberapa amalan terbaik untuk melaksanakan tanda matematik dengan berkesan:
- Ketahui makna dan fungsi setiap tanda: Sebelum anda menggunakan sebarang tanda, pastikan anda memahami apa yang diwakilinya dan bagaimana ia digunakan.
- Gunakan tanda dengan konsisten: Konsistensi adalah penting dalam matematik. Gunakan tanda yang sama untuk mewakili konsep yang sama sepanjang kerja anda.
- Ikut konvensyen dan peraturan: Terdapat peraturan dan konvensyen tertentu yang mengawal penggunaan tanda matematik. Pastikan anda mematuhinya untuk mengelakkan kesilapan.
- Amalkan, amalkan, amalkan: Cara terbaik untuk menguasai tanda matematik adalah dengan menggunakannya secara kerap. Selesaikan masalah, baca buku teks, dan berlatih menulis formula.
- Jangan takut untuk bertanya: Jika anda tidak pasti tentang sesuatu, jangan takut untuk bertanya kepada guru, tutor, atau rakan anda.
Contoh Nyata Tanda Matematik
Berikut adalah beberapa contoh nyata tanda matematik yang digunakan dalam pelbagai bidang:
- Fizik: E=mc², formula terkenal Albert Einstein yang menghubungkan tenaga (E), jisim (m), dan kelajuan cahaya (c).
- Ekonomi: Qd = a - bP, persamaan permintaan yang menunjukkan hubungan antara kuantiti diminta (Qd), harga (P), dan faktor lain (a dan b).
- Kejuruteraan: F = ma, hukum gerakan Newton kedua yang menghubungkan daya (F), jisim (m), dan pecutan (a).
- Statistik: σ = √Σ(xᵢ - μ)²/N, formula untuk sisihan piawai (σ), yang mengukur penyebaran data di sekitar min (μ).
- Sains komputer: if (x > 0) { print("Positif"); } else { print("Negatif"); }, contoh kod yang menggunakan pernyataan bersyarat untuk memeriksa sama ada nombor positif atau negatif.
Cabaran dan Penyelesaian Tanda Matematik
Berikut adalah beberapa cabaran biasa yang dihadapi orang ramai dengan tanda matematik dan beberapa penyelesaian yang mungkin:
| Cabaran | Penyelesaian |
|---|---|
| Menghafal semua tanda | Fokus pada memahami konsep dan menggunakan kad imbas atau alat pembelajaran dalam talian untuk menghafal. |
| Memahami makna tanda dalam konteks yang berbeza | Amalkan menyelesaikan masalah dari pelbagai bidang dan rujuk buku teks atau sumber lain untuk penjelasan. |
| Menulis formula dengan betul | Berhati-hati dengan susunan operasi dan gunakan tanda kurung apabila perlu. |
| Menggunakan kalkulator saintifik | Ketahui fungsi kalkulator anda dan amalkan menggunakannya untuk pelbagai pengiraan. |
| Mengatasi kebimbangan matematik | Cari sokongan daripada guru, tutor, atau rakan sebaya, dan amalkan teknik pengurusan tekanan. |
Soalan Lazim tentang Tanda Matematik
Berikut adalah beberapa soalan lazim tentang tanda matematik:
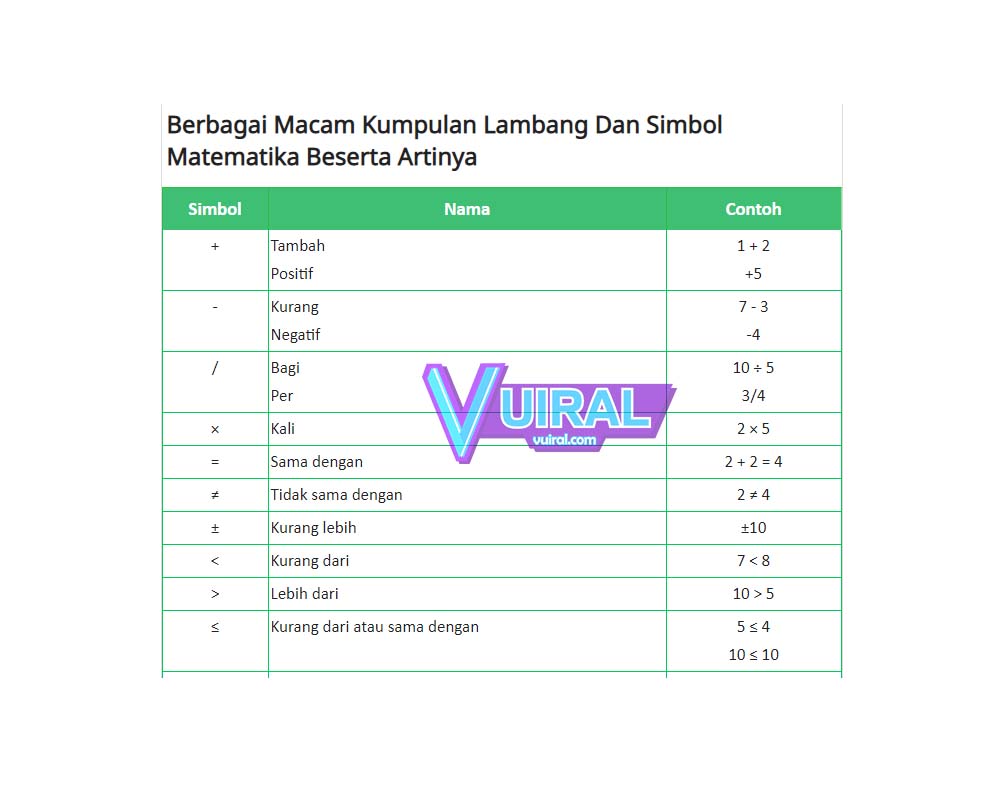
- Apakah perbezaan antara tanda tambah (+) dan tolak (-)? Tanda tambah menunjukkan penambahan, manakala tanda tolak menunjukkan penolakan.
- Apakah maksud tanda sama dengan (=)? Tanda sama dengan menunjukkan bahawa dua kuantiti adalah sama.
- Apakah perbezaan antara tanda lebih besar daripada (>) dan kurang daripada (<)? Tanda lebih besar daripada menunjukkan bahawa kuantiti di sebelah kiri lebih besar daripada kuantiti di sebelah kanan. Tanda kurang daripada menunjukkan bahawa kuantiti di sebelah kiri kurang daripada kuantiti di sebelah kanan.
- Apakah maksud tanda peratusan (%)? Tanda peratusan menunjukkan pecahan daripada seratus.
- Apakah maksud tanda pi (π)? Tanda pi mewakili nisbah lilitan bulatan kepada diameternya, yang kira-kira 3.14159.
- Apakah maksud tanda infiniti (∞)? Tanda infiniti mewakili kuantiti yang tidak terhingga.
- Apakah perbezaan antara tanda kamiran (∫) dan pembezaan (d/dx)? Tanda kamiran digunakan untuk mencari luas di bawah lengkung, manakala tanda pembezaan digunakan untuk mencari cerun lengkung pada titik tertentu.
- Apakah maksud tanda sigma (Σ)? Tanda sigma digunakan untuk mewakili penjumlahan siri nombor.
Tips dan Trik Tanda Matematik
Berikut adalah beberapa tips dan trik untuk menguasai tanda matematik:
- Cipta kad imbas dengan tanda di satu sisi dan definisi di sisi lain.
- Gunakan mnemonik dan rima untuk menghafal formula dan tanda.
- Tulis formula dan definisi berulang kali untuk meningkatkan ingatan otot.
- Cari video dan tutorial dalam talian yang menerangkan konsep matematik dengan cara yang mudah difahami.
- Sertai kumpulan belajar atau forum dalam talian untuk berhubung dengan pelajar lain dan bertukar idea.
Kesimpulannya, tanda dalam rumus matematik adalah penting untuk memahami dan berkomunikasi idea matematik. Menguasai tanda-tanda ini mungkin kelihatan sukar pada mulanya, tetapi dengan kesabaran, amalan, dan sumber yang betul, anda boleh membuka kunci kepada dunia matematik yang menakjubkan. Ingat, setiap tanda adalah seperti kunci yang membuka pintu kepada pengetahuan dan pemahaman baharu. Teruskan meneroka, terus bertanya, dan jangan takut untuk membuat kesilapan - itu adalah sebahagian daripada proses pembelajaran! Semoga berjaya dalam perjalanan matematik anda!
Rahsia tersembunyi di bawah kaki anda panduan lengkap muat turun peta geologi regional
Misteri plat nomor bm terungkai daerah mana pemiliknya berasal
Astro call centre number
Apa Itu Matematika Diskrit - You're The Only One I've Told
Tanda Sama Dengan Dalam Matematika - You're The Only One I've Told
Rumus Perkalian di Excel: Simbol (*) Hingga Fungsi PRODUCT - You're The Only One I've Told
Tanda Lebih Besar Dan Lebih Kecil Dalam Matematika - You're The Only One I've Told
Belajar Notasi Sigma beserta Rumusnya, Yuk! - You're The Only One I've Told
Arti Tanda Dalam Matematika - You're The Only One I've Told
Lambang Lambang Dalam Fisika - You're The Only One I've Told
tanda dalam rumus matematika - You're The Only One I've Told
tanda dalam rumus matematika - You're The Only One I've Told
Detail Simbol Tegak Lurus Koleksi Nomer 13 - You're The Only One I've Told
Pengertian, Sifat dan Rumus Notasi Sigma Matematika - You're The Only One I've Told
tanda dalam rumus matematika - You're The Only One I've Told
Arti Simbol Dalam Matematika - You're The Only One I've Told