Pernahkah anda terserempak dengan simbol aneh yang seakan-akan "E" terbalik ketika melayari dunia matematik? Jangan risau, anda tidak keseorangan! Simbol unik ini, yang dikenali sebagai "kuantor eksistensial," merupakan antara simbol asas dalam logik predikat dan teori set.
Meskipun rupa bentuknya ringkas, "kuantor eksistensial" memainkan peranan penting dalam bahasa matematik. Ia berfungsi untuk menyatakan kewujudan sesuatu objek atau elemen dalam set atau domain tertentu. Bayangkan cuba untuk menerangkan kewujudan sesuatu tanpa menggunakan perkataan "ada" atau "wujud"—pastinya sukar, bukan? Di sinilah "kuantor eksistensial" menjadi penyelamat!
Penggunaan "kuantor eksistensial" menjangkau pelbagai bidang dalam matematik, dari algebra dan kalkulus hingga kepada sains komputer dan statistik. Dalam setiap bidang ini, simbol ini membantu kita merumuskan konsep dengan lebih tepat dan ringkas.
Artikel ini akan membongkar misteri di sebalik "kuantor eksistensial" dengan menelusuri sejarah, definisi, dan kepentingannya. Kami juga akan meneroka bagaimana simbol ini diaplikasikan dalam pelbagai bidang matematik, disertai dengan contoh-contoh mudah untuk pemahaman yang lebih jelas.
Jadi, bersiap sedia untuk menyelami dunia "kuantor eksistensial" dan temui bagaimana simbol ringkas ini mampu merevolusikan cara kita berfikir tentang kewujudan dalam konteks matematik!
Kelebihan dan Kekurangan "Kuantor Eksistensial"
Seperti kebanyakan konsep matematik, "kuantor eksistensial" juga mempunyai kelebihan dan kekurangannya yang tersendiri.
| Kelebihan | Kekurangan |
|---|---|
| Memudahkan pernyataan kewujudan objek matematik. | Tidak memberikan maklumat khusus tentang objek yang wujud. |
| Membuat pernyataan matematik lebih ringkas dan tepat. | Boleh mengelirukan jika tidak digunakan dengan betul. |
Amalan Terbaik Menggunakan "Kuantor Eksistensial"
- Fahami konteks: Pastikan anda memahami dengan jelas domain atau set yang sedang dibincangkan sebelum menggunakan "kuantor eksistensial".
- Gunakan dengan tepat: Pastikan "kuantor eksistensial" digunakan hanya untuk menyatakan kewujudan, bukan untuk kuantifikasi lain seperti "semua" atau "beberapa".
- Jelaskan pemboleh ubah: Pastikan pemboleh ubah yang digunakan bersama "kuantor eksistensial" didefinisikan dengan jelas.
- Gunakan tanda kurung dengan betul: Tanda kurung penting untuk mengelakkan kekeliruan tentang skop "kuantor eksistensial".
- Berlatih: Amalan berterusan akan membantu anda menguasai penggunaan "kuantor eksistensial" dengan lebih baik.
Soalan Lazim Mengenai "Kuantor Eksistensial"
Berikut adalah beberapa soalan lazim mengenai "kuantor eksistensial":
- Apakah perbezaan antara "kuantor eksistensial" dan "kuantor universal"?
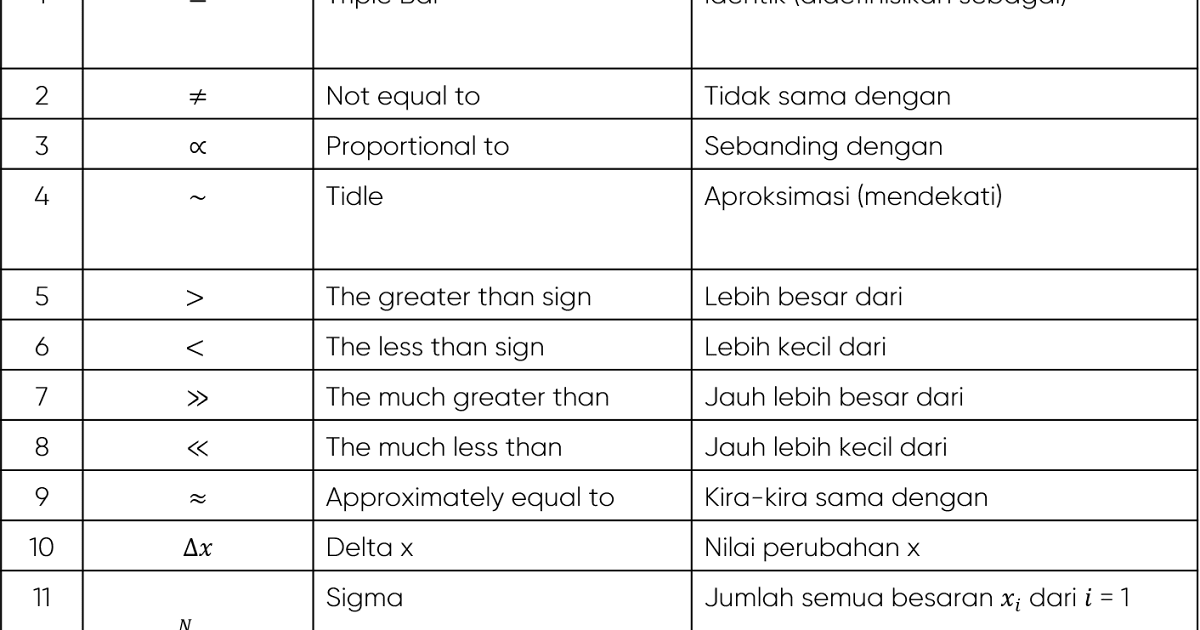
"Kuantor eksistensial" (∃) menyatakan kewujudan sekurang-kurangnya satu objek, manakala "kuantor universal" (∀) menyatakan bahawa sesuatu adalah benar untuk semua objek dalam domain.
- Bolehkah "kuantor eksistensial" digunakan bersama-sama dengan "kuantor universal"?
Ya, kedua-dua kuantor ini boleh digunakan bersama untuk membentuk pernyataan yang lebih kompleks.
- Apakah kepentingan "kuantor eksistensial" dalam matematik?
"Kuantor eksistensial" membolehkan kita menyatakan konsep kewujudan dengan tepat dan ringkas, yang penting dalam pelbagai bidang matematik.
Tips dan Trik Menggunakan "Kuantor Eksistensial"
- Bayangkan "kuantor eksistensial" sebagai "pemburu harta" yang mencari sekurang-kurangnya satu objek yang memenuhi syarat tertentu.
- Gunakan contoh-contoh konkrit untuk membantu memahami konsep abstrak yang berkaitan dengan "kuantor eksistensial".
- Jangan takut untuk meminta bantuan jika anda menghadapi kesukaran memahami "kuantor eksistensial".
Sebagai kesimpulan, "kuantor eksistensial" atau simbol "E terbalik" merupakan elemen penting dalam bahasa matematik. Walaupun kelihatan aneh pada mulanya, pemahaman tentang simbol ini membuka pintu kepada pemahaman yang lebih mendalam tentang konsep kewujudan dalam matematik. Dengan menguasai penggunaannya, kita dapat mengungkap lebih banyak rahsia dan keindahan yang tersembunyi di sebalik dunia matematik yang penuh misteri ini.
Latihan sejarah tahun 5 mengikut topik
Haiwan unik tanpa segmen meneroka dunia cacing dan ubur ubur
Rahsia menguasai karangan bm tingkatan 5 panduan lengkap contoh
Flow Chart Arti Simbol - You're The Only One I've Told
Simbol Data Pada Flowchart - You're The Only One I've Told
lambang e terbalik dalam matematika - You're The Only One I've Told
Detail Lambang Lambang Dalam Matematika Koleksi Nomer 40 - You're The Only One I've Told
Contoh Simbol Dan Artinya Arti Lambang Dan Simbol Simbol M - You're The Only One I've Told
Detail Lambang Lambang Dalam Matematika Koleksi Nomer 8 - You're The Only One I've Told
Detail Lambang Lambang Dalam Matematika Koleksi Nomer 6 - You're The Only One I've Told
lambang e terbalik dalam matematika - You're The Only One I've Told
lambang e terbalik dalam matematika - You're The Only One I've Told
lambang e terbalik dalam matematika - You're The Only One I've Told
Detail Lambang Lambang Dalam Matematika Koleksi Nomer 8 - You're The Only One I've Told
lambang e terbalik dalam matematika - You're The Only One I've Told
Detail Lambang Lambang Dalam Matematika Koleksi Nomer 11 - You're The Only One I've Told