Bayangkan dunia tanpa bola. Tiada lagi permainan bola sepak yang mengujakan, tiada lagi glob yang memaparkan keindahan bumi, dan mungkin juga, tiada lagi planet yang kita diami! Bola, dengan bentuknya yang unik dan ciri-ciri geometri yang menarik, memainkan peranan penting dalam kehidupan kita, dari aspek rekreasi hingga kepada sains dan teknologi.
Tetapi, apakah yang menjadikan bola begitu istimewa? Jawapannya terletak pada ciri-ciri geometri yang dimilikinya. Tidak seperti bentuk geometri lain seperti kubus atau piramid yang mempunyai sisi rata dan bucu yang tajam, bola hanya mempunyai satu permukaan melengkung yang licin. Permukaan melengkung ini memberikan bola beberapa ciri unik yang menjadikannya objek yang menarik untuk dikaji dan diaplikasikan dalam pelbagai bidang.
Ciri utama bola yang paling ketara adalah kesimetriannya yang sempurna. Setiap titik di permukaan bola adalah sama jaraknya dari pusat bola. Ciri ini menjadikan bola objek yang stabil dan seimbang, sesuai digunakan dalam pelbagai aplikasi seperti bearing dan roda. Selain itu, bentuk sfera bola juga memberikannya nisbah isipadu kepada luas permukaan yang paling besar berbanding dengan bentuk geometri lain. Ini bermakna bola boleh memuatkan isipadu maksimum dengan menggunakan luas permukaan minimum, ciri yang sangat berguna dalam reka bentuk tangki simpanan dan belon udara panas.
Keunikan ciri-ciri bola telah menarik minat manusia sejak zaman kuno lagi. Ahli falsafah Yunani kuno seperti Plato dan Aristotle telah mengkaji sifat-sifat sfera dan mengagumi kesempurnaan bentuknya. Pada abad ke-3 SM, Archimedes, seorang ahli matematik dan fizik Yunani, menemui formula untuk mengira isipadu dan luas permukaan sfera, satu pencapaian luar biasa dalam sejarah matematik.
Walaupun bola kelihatan seperti objek yang mudah, namun memahami ciri-ciri uniknya membuka pintu kepada pelbagai aplikasi dalam kehidupan seharian kita. Daripada reka bentuk bangunan dan kenderaan yang aerodinamik hinggalah kepada teknologi nano dan penerokaan angkasa lepas, bola dan ciri-ciri geometriknya terus memainkan peranan penting dalam membentuk dunia moden kita.
Walaupun tidak mempunyai sisi atau bucu, sfera mempunyai ciri-ciri yang unik dan menarik:
- Permukaan Lengkung Seragam: Seluruh permukaan sfera melengkung sama rata, tanpa sebarang sudut atau tepi.
- Jarak Pusat Sama: Setiap titik di permukaan sfera berada pada jarak yang sama dari pusatnya, dikenali sebagai jejari.
- Nisbah Isipadu-Luas Maksimum: Sfera mempunyai nisbah isipadu kepada luas permukaan terbesar berbanding sebarang bentuk geometri lain.
Contoh bola dalam kehidupan seharian termasuklah bola sepak, glob, manik, dan planet.
Kelebihan dan Kekurangan Ciri-ciri Bola
| Kelebihan | Kekurangan |
|---|---|
| Sangat stabil dan seimbang | Boleh bergolek dengan mudah |
| Mempunyai nisbah isipadu kepada luas permukaan yang tinggi | Sukar disimpan dan disusun |
| Aerodinamik | Sukar dipegang dengan kuat |
Amalan Terbaik untuk Mengaplikasikan Ciri-ciri Bola
- Reka Bentuk Aerodinamik: Gunakan bentuk sfera untuk mengurangkan seretan dan meningkatkan kecekapan bahan api dalam kenderaan dan pesawat.
- Kecekapan Penyimpanan: Manfaatkan nisbah isipadu-luas sfera yang tinggi untuk memaksimumkan kapasiti penyimpanan dalam tangki dan bekas.
- Kestabilan dan Keseimbangan: Gunakan bentuk sfera dalam bearing dan roda untuk memastikan pergerakan yang lancar dan stabil.
- Estetika dan Reka Bentuk: Integrasikan bentuk sfera ke dalam seni bina, reka bentuk produk, dan fesyen untuk estetika yang menyenangkan.
- Aplikasi Sukan dan Rekreasi: Gunakan bentuk sfera dalam pelbagai sukan seperti bola sepak, bola keranjang, dan tenis untuk permainan yang dinamik dan menarik.
Contoh Nyata Ciri-ciri Bola
- Glob: Mewakili Bumi dengan tepat dan memaparkan benua, lautan, dan negara dengan betul.
- Bola Sepak: Direka untuk pergerakan yang lancar dan aerodinamik, sesuai untuk ditendang dan dikawal.
- Manik: Digunakan dalam barang kemas dan hiasan kerana bentuknya yang menarik dan simetri.
- Planet: Menunjukkan bagaimana graviti membentuk objek besar di angkasa menjadi bentuk sfera.
- Galas Bebola: Mengurangkan geseran dan membolehkan putaran lancar dalam mesin dan peralatan.
Cabaran dan Penyelesaian Berkaitan Ciri-ciri Bola
- Cabaran: Sukar menyimpan dan menyusun sfera dengan cekap.
Penyelesaian: Gunakan bekas yang direka khas atau sistem pembungkusan untuk menyimpan sfera dengan selamat dan teratur. - Cabaran: Sfera boleh bergolek dengan mudah, yang boleh menjadi masalah dalam sesetengah situasi.
Penyelesaian: Cipta permukaan rata pada sfera atau gunakan penghadang untuk mengelakkan pergerakan yang tidak diingini. - Cabaran: Sfera sukar dipegang dengan kuat kerana bentuknya yang licin.
Penyelesaian: Tambah tekstur atau cengkaman pada permukaan sfera, atau gunakan pemegang yang direka khas. - Cabaran: Mengukur isipadu dan luas permukaan sfera dengan tepat boleh menjadi sukar.
Penyelesaian: Gunakan formula geometri dan alat pengukur yang tepat untuk mendapatkan pengukuran yang tepat. - Cabaran: Memotong dan membentuk sfera dengan tepat boleh menjadi mencabar.
Penyelesaian: Gunakan alat pemotong dan pembentukan khas yang direka untuk bahan dan saiz sfera tertentu.
Soalan Lazim
1. Apakah definisi sfera?
Sfera ialah set semua titik dalam ruang tiga dimensi yang sama jaraknya dari satu titik yang dipanggil pusat.
2. Apakah perbezaan antara sfera dan bulatan?
Bulatan ialah bentuk dua dimensi manakala sfera ialah bentuk tiga dimensi.
3. Apakah beberapa aplikasi praktikal sfera?
Sfera digunakan dalam pelbagai aplikasi, termasuk galas bebola, tangki simpanan, sukan, dan seni bina.
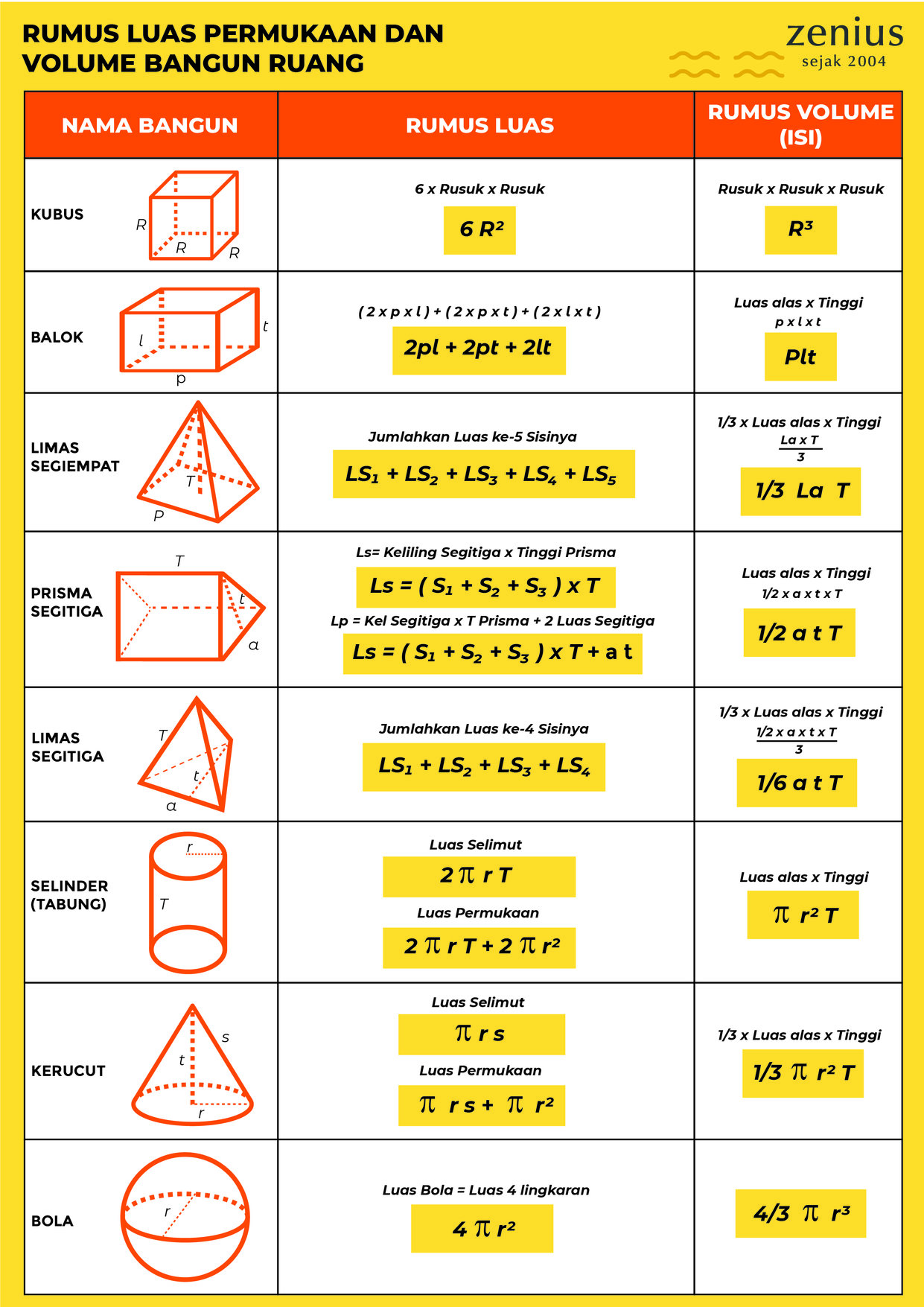
4. Apakah formula untuk mengira isipadu sfera?
Isipadu sfera = (4/3)πr³, dengan r ialah jejari.
5. Apakah formula untuk mengira luas permukaan sfera?
Luas permukaan sfera = 4πr², dengan r ialah jejari.
6. Mengapa sfera digunakan dalam sukan seperti bola sepak dan bola keranjang?
Bentuk sfera membolehkan bola bergerak dengan lancar dan dalam pelbagai arah.
7. Apakah kepentingan sfera dalam astronomi?
Planet dan bintang berbentuk sfera kerana graviti.
8. Apakah beberapa contoh sfera dalam alam semula jadi?
Contoh sfera dalam alam semula jadi termasuklah buah-buahan seperti oren dan tembikai, serta titisan air.
Tips dan Trik
- Gunakan model 3D atau perisian visualisasi untuk lebih memahami ciri-ciri sfera.
- Jalankan eksperimen mudah dengan bola untuk meneroka sifat fizikalnya, seperti pergerakan dan keseimbangan.
- Kaji aplikasi sfera dalam pelbagai bidang seperti seni bina, kejuruteraan, dan reka bentuk.
Sebagai kesimpulan, sfera dengan ciri-cirinya yang unik seperti permukaan melengkung seragam, jarak pusat yang sama, dan nisbah isipadu kepada luas permukaan yang optimum, menawarkan pelbagai manfaat dan aplikasi praktikal dalam kehidupan seharian kita. Dari reka bentuk aerodinamik kepada kecekapan penyimpanan dan estetika yang menarik, sfera terus memainkan peranan penting dalam pelbagai bidang, daripada teknologi hinggalah kepada seni dan rekreasi. Memahami dan menghargai ciri-ciri unik sfera membolehkan kita untuk terus berinovasi dan mencipta penyelesaian baru untuk cabaran dunia moden.
Diploma teknologi maklumat teknologi digital
Rahsia nama nama negeri di malaysia dari mana asalnya
Burung garuda png hitam putih simbol kebanggaan yang kekal
Bangun Ruang: Jenis, Gambar, Ciri, Rumus dan Contoh Soal - You're The Only One I've Told
ciri bangun ruang bola - You're The Only One I've Told
ciri bangun ruang bola - You're The Only One I've Told
Soal Bangun Ruang Kelas 2 - You're The Only One I've Told
ciri bangun ruang bola - You're The Only One I've Told
ciri bangun ruang bola - You're The Only One I've Told
Rumus Bangun Ruang Kerucut Beserta Contoh Soalnya - You're The Only One I've Told
Daftar Lengkap Rumus Bangun Ruang (Kubus, Balok, Tabung, Bola, Dll - You're The Only One I've Told
ciri bangun ruang bola - You're The Only One I've Told
Soal Volume Bangun Ruang - You're The Only One I've Told
ciri bangun ruang bola - You're The Only One I've Told
Ciri ciri bangun ruang - You're The Only One I've Told
Rumus Kerucut : Pengertian, Ciri, Sifat, Unsur dan Contoh Soalnya - You're The Only One I've Told
ciri bangun ruang bola - You're The Only One I've Told
Rumus Bangun Ruang Menghitung Volume Luas Permukaan Dan Contoh Soal - You're The Only One I've Told