Stell dir vor, du hast einen Geburtstagskuchen und musst ihn genau in der Mitte durchschneiden, damit beide Hälften gleich groß sind. Genau das bedeutet "halbieren" in der Mathematik – etwas in zwei gleiche Teile teilen. Klingt erstmal einfach, oder? Aber "halbieren" geht weit über Kuchen schneiden hinaus und spielt in der Geometrie eine wichtige Rolle.
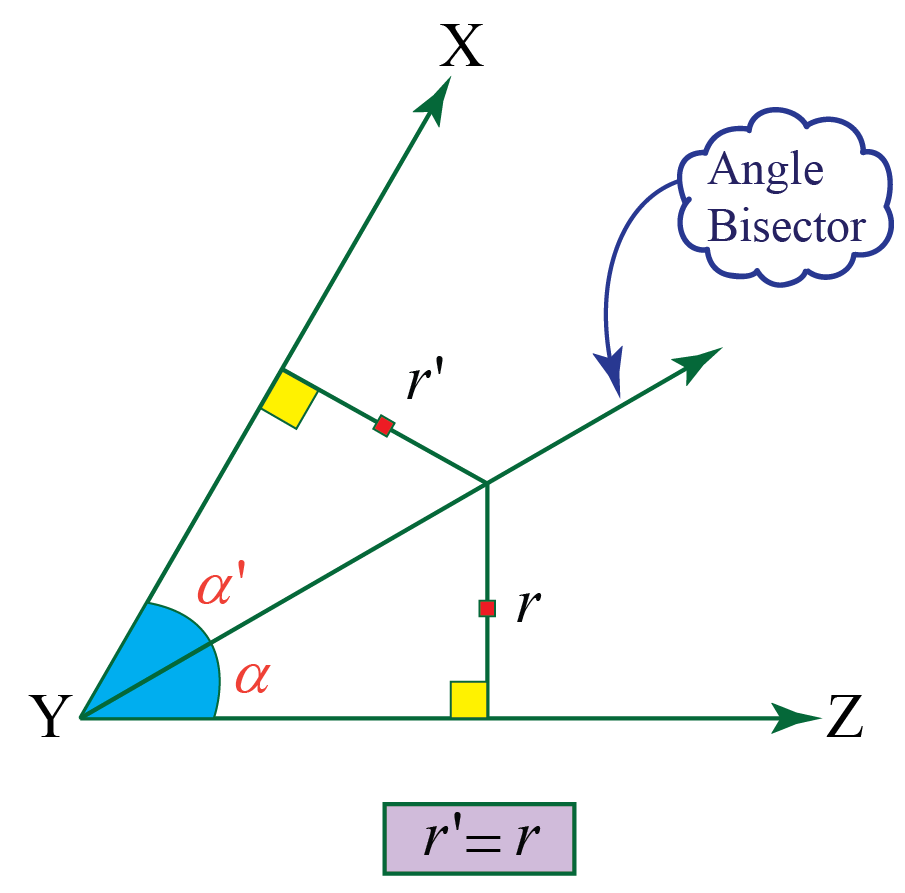
In der Welt der Mathematik bedeutet "halbieren" nicht nur, etwas in zwei Hälften zu teilen, sondern es ganz präzise mit geometrischen Konstruktionen zu tun. Eine der häufigsten Anwendungen ist das Halbieren von Winkeln und Strecken. Stell dir vor, du musst einen Winkel in zwei gleiche Winkel aufteilen. Mit Zirkel und Lineal kannst du eine sogenannte Winkelhalbierende konstruieren, die genau durch die Mitte des Winkels verläuft.
Die Geschichte des Halbierens reicht weit zurück. Schon die alten Griechen beschäftigten sich mit geometrischen Konstruktionen und entwickelten Methoden, um Winkel und Strecken präzise zu halbieren. Diese Erkenntnisse waren grundlegend für die Entwicklung der Geometrie und finden noch heute Anwendung in vielen Bereichen, von der Architektur bis zur Computergrafik.
Doch wozu das Ganze? Das Halbieren von Winkeln und Strecken mag im ersten Moment abstrakt erscheinen, hat aber viele praktische Anwendungen. In der Architektur werden diese Konstruktionen verwendet, um beispielsweise symmetrische Gebäude zu entwerfen oder komplexe Formen zu konstruieren. Auch in der Navigation und Kartografie spielen geometrische Konstruktionen, einschließlich des Halbierens, eine wichtige Rolle.
Ein einfaches Beispiel für das Halbieren im Alltag ist das Falten eines Blattes Papier. Wenn du das Blatt genau in der Mitte faltest, so dass die gegenüberliegenden Seiten aufeinanderliegen, hast du die Kante des Blattes halbiert. Du hast eine Linie erzeugt, die durch den Mittelpunkt der Kante verläuft und diese in zwei gleiche Teile teilt. Das mag trivial erscheinen, verdeutlicht aber das Prinzip des Halbierens: die exakte Teilung eines Objekts in zwei gleiche Hälften.
Vorteile des Halbierens in der Mathematik
Das Halbieren bietet in der Mathematik zahlreiche Vorteile:
- Präzision: Es ermöglicht exakte Teilungen von Strecken und Winkeln.
- Konstruktionshilfe: Es dient als Grundlage für komplexere geometrische Konstruktionen.
- Anwendungsvielfalt: Es findet Anwendung in vielen Bereichen, von der Architektur bis zur Informatik.
Nachteile des Halbierens in der Mathematik
Obwohl das Halbieren viele Vorteile bietet, gibt es auch ein paar Herausforderungen:
| Herausforderung | Lösung |
|---|---|
| Ungenauigkeiten bei der manuellen Konstruktion | Verwendung von präzisen Instrumenten und sorgfältiges Arbeiten |
| Begrenzte Anwendbarkeit auf komplexe Kurven | Nutzung von numerischen Methoden in der Computergrafik |
Häufige Fragen zum Halbieren
Hier sind einige häufig gestellte Fragen zum Halbieren in der Mathematik:
- Was bedeutet "halbieren" in der Mathematik?
"Halbieren" bedeutet, etwas in zwei gleiche Teile zu teilen, sei es eine Strecke, ein Winkel oder ein anderes geometrisches Objekt.
- Wie halbiert man einen Winkel mit Zirkel und Lineal?
Um einen Winkel zu halbieren, zeichnest du mit dem Zirkel einen Kreisbogen um den Scheitelpunkt des Winkels. Die Schnittpunkte des Kreisbogens mit den Schenkeln des Winkels markierst du. Zeichne nun mit dem Zirkel zwei weitere Kreisbögen, jeweils mit dem gleichen Radius, um die beiden markierten Schnittpunkte. Der Schnittpunkt dieser beiden Kreisbögen liegt auf der Winkelhalbierenden. Verbinde den Scheitelpunkt des Winkels mit diesem Schnittpunkt, um die Winkelhalbierende zu konstruieren.
Tipps und Tricks zum Halbieren
Hier sind ein paar hilfreiche Tipps zum Halbieren:
- Verwende immer präzise Instrumente wie einen guten Zirkel und ein Lineal.
- Übe die Konstruktionsschritte, um sicherer zu werden.
- Nutze Online-Ressourcen und Videos, um das Konzept besser zu verstehen.
Fazit
Das Halbieren mag auf den ersten Blick wie ein einfaches mathematisches Konzept erscheinen, spielt aber eine wichtige Rolle in der Geometrie und vielen anderen Bereichen. Von der Konstruktion symmetrischer Gebäude bis zur Entwicklung von Computerspielen – das Halbieren ist ein grundlegendes Werkzeug, das uns hilft, die Welt um uns herum zu verstehen und zu gestalten. Auch wenn es manchmal knifflig sein kann, die Konstruktionen präzise durchzuführen, lohnt es sich, die Prinzipien des Halbierens zu verstehen und anzuwenden. Wer weiß, vielleicht entdeckst du ja selbst neue Anwendungsmöglichkeiten für dieses faszinierende mathematische Konzept!
Witzige partnerprofile mit serienmotiven der ultimative guide
Berlin tag und nacht folge verpasst schau sie kostenlos online
Zakat hilfe in sabah unterstutzung fur bedurftige
what is the meaning of bisect in maths - You're The Only One I've Told
Bisecting Intervals and Angles - You're The Only One I've Told
Perpendicular Bisector Theorem Worksheet Pdf - You're The Only One I've Told
bisect, bisector ~ A Maths Dictionary for Kids Quick Reference by Jenny - You're The Only One I've Told
Angle Bisector Theorem Formula - You're The Only One I've Told
Quqdrilateral ABCD is a parallelogram take a point e on the side AB - You're The Only One I've Told
Bisect: Meaning, Formula, Examples, Facts - You're The Only One I've Told
All The Properties Of A Rectangle - You're The Only One I've Told
:max_bytes(150000):strip_icc()/common-mathematic-symbols-2312232_final_CORRECTED-d1b3858039ce4668b3ae0b028da7a258.png)
Common Symbols In Math - You're The Only One I've Told
Math Symbols: List of 35+ Useful Mathematical Symbols and their Names - You're The Only One I've Told
Angle Bisector Theorem Calculator - You're The Only One I've Told
Definition of Angle Bisector - You're The Only One I've Told
Segment Bisector Real Life Example - You're The Only One I've Told
Bisector Of An Angle - You're The Only One I've Told
Bisect: Meaning, Formula, Examples, Facts - You're The Only One I've Told