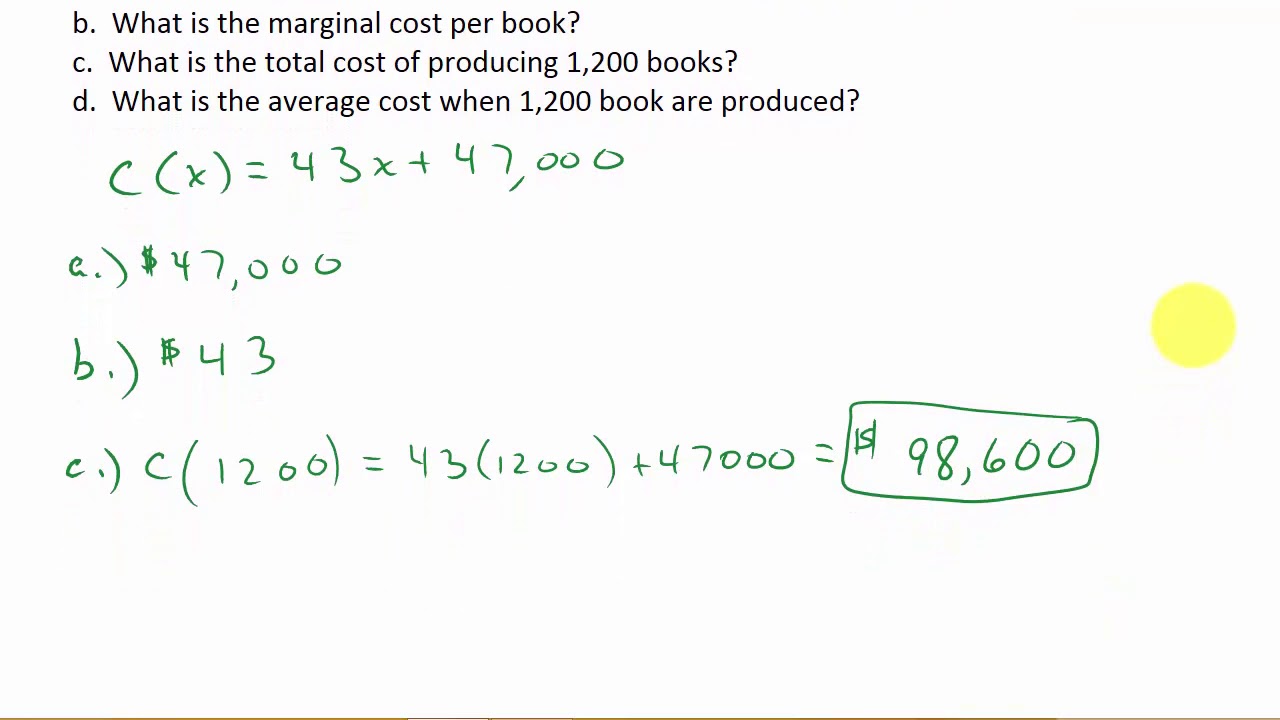Wie können Unternehmen ihre Produktionskosten effektiv steuern und minimieren? Die Antwort liegt oft in der Analyse der Grenzkosten der Durchschnittskosten. Dieses Konzept, oft als "Grenzkostenfunktion der Durchschnittskosten" bezeichnet, bietet wertvolle Einblicke in die Kostenstruktur und ermöglicht fundierte Entscheidungen zur Produktionsmenge.
Die Grenzkostenfunktion der Durchschnittskosten beschreibt, wie sich die durchschnittlichen Kosten pro produzierter Einheit verändern, wenn eine zusätzliche Einheit hergestellt wird. Sie hilft Unternehmen, den Punkt zu identifizieren, an dem die Produktion einer weiteren Einheit die durchschnittlichen Kosten minimal beeinflusst, und somit die optimale Produktionsmenge zu bestimmen. Ein tiefes Verständnis dieser Funktion ist für Unternehmen jeder Größe unerlässlich.
Die Formel zur Berechnung der Grenzkostenfunktion der Durchschnittskosten leitet sich aus der Kostenfunktion ab. Die Kostenfunktion beschreibt die Gesamtkosten der Produktion in Abhängigkeit von der produzierten Menge. Die Durchschnittskosten ergeben sich aus der Division der Gesamtkosten durch die Menge. Die Grenzkostenfunktion der Durchschnittskosten wird berechnet, indem man die Ableitung der Durchschnittskostenfunktion nach der Menge bildet.
Die Grenzkostenfunktion der Durchschnittskosten ist ein mächtiges Werkzeug für die Kostenkontrolle. Durch die Analyse dieser Funktion können Unternehmen Bereiche identifizieren, in denen Kosteneinsparungen möglich sind, und fundierte Entscheidungen über Produktionsmengen, Preisgestaltung und Investitionen treffen. Die Kenntnis der zugrundeliegenden Mathematik und der Interpretation der Ergebnisse ist dabei entscheidend.
In diesem Artikel werden wir die Grenzkostenfunktion der Durchschnittskosten genauer untersuchen und ihre praktische Anwendung in der Unternehmensführung erläutern. Wir werden die Formel, Beispiele und bewährte Verfahren zur Implementierung dieser Funktion diskutieren und Ihnen helfen, dieses wichtige Instrument für Ihre strategische Entscheidungsfindung zu nutzen.
Historisch betrachtet entwickelte sich die Grenzkostenfunktion der Durchschnittskosten aus der Notwendigkeit, Produktionskosten zu optimieren. Im 19. Jahrhundert, mit dem Aufkommen der Industrialisierung, wurde es immer wichtiger, die Kosten zu verstehen und zu kontrollieren. Die Grenzkostenanalyse entwickelte sich als Teil der neoklassischen Wirtschaftstheorie und bietet ein Instrument zur Bestimmung der optimalen Produktionsmenge.
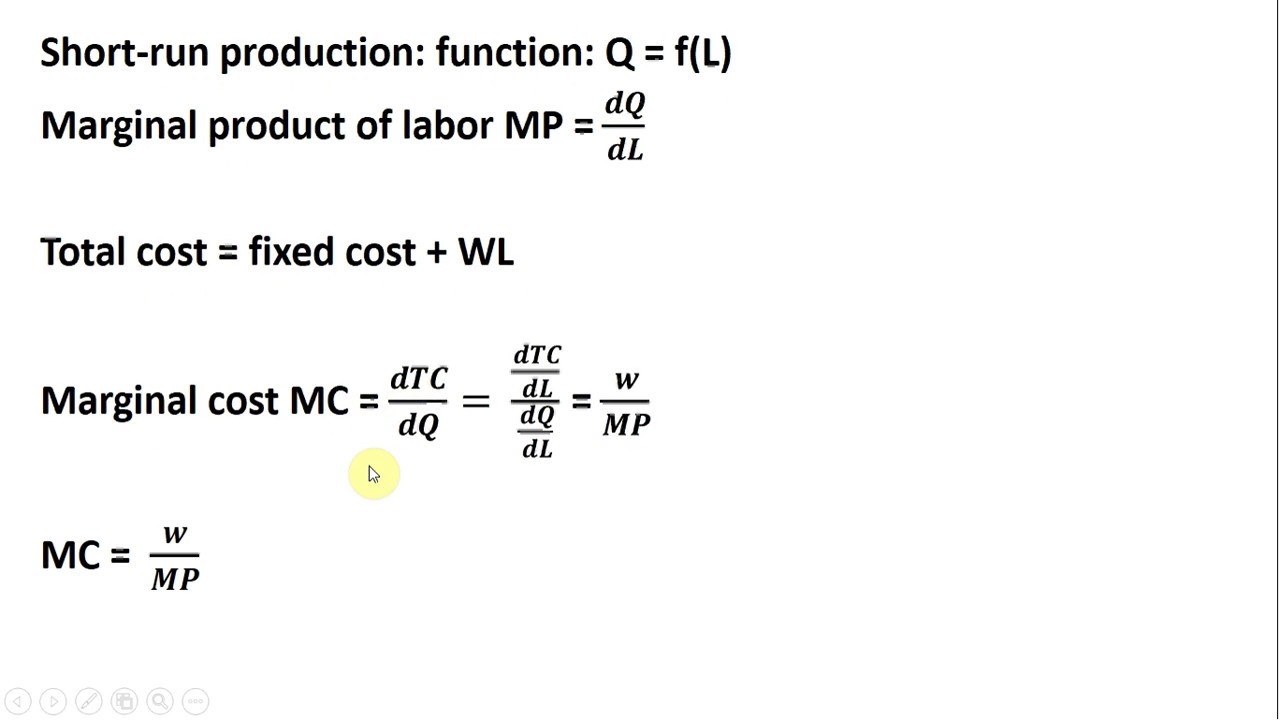
Die Grenzkostenfunktion der Durchschnittskosten (GKDAK) wird berechnet, indem die Ableitung der Durchschnittskostenfunktion nach der Menge genommen wird. Die Durchschnittskostenfunktion (DAK) berechnet sich als Gesamtkosten (K) geteilt durch die Menge (x): DAK(x) = K(x)/x. Die GKDAK ist dann DAK'(x).
Ein einfaches Beispiel: Angenommen, die Kostenfunktion ist K(x) = 2x² + 10x + 50. Die DAK-Funktion ist dann DAK(x) = (2x² + 10x + 50)/x = 2x + 10 + 50/x. Die GKDAK ist DAK'(x) = 2 - 50/x².
Vorteile der Anwendung der GKDAK sind: 1. Optimierung der Produktionsmenge für minimale Durchschnittskosten. 2. Verbesserte Preisgestaltungsstrategien. 3. Effektivere Ressourcenallokation.
Häufig gestellte Fragen: 1. Was ist die Formel für die GKDAK? - Die Ableitung der Durchschnittskostenfunktion. 2. Wie wird sie berechnet? - Durch Ableiten der DAK-Funktion. 3. Wozu dient sie? - Zur Kostenminimierung.
Tipps: Verwenden Sie Software zur Berechnung. Interpretieren Sie die Ergebnisse sorgfältig.
Zusammenfassend lässt sich sagen, dass die Grenzkostenfunktion der Durchschnittskosten ein wichtiges Instrument für Unternehmen ist, um ihre Kosten zu verstehen und zu optimieren. Durch die Analyse dieser Funktion können Unternehmen fundierte Entscheidungen über Produktionsmengen, Preisgestaltung und Investitionen treffen und so ihre Wettbewerbsfähigkeit steigern. Es ist wichtig, die Formel zu verstehen, die Ergebnisse korrekt zu interpretieren und die GKDAK in Kombination mit anderen betriebswirtschaftlichen Instrumenten zu verwenden, um eine umfassende Kostenkontrolle zu gewährleisten. Investieren Sie Zeit in das Verständnis dieses Konzepts – es zahlt sich aus! Ein tieferes Verständnis der Kostenstruktur und die Fähigkeit, die optimale Produktionsmenge zu bestimmen, sind entscheidend für den langfristigen Erfolg eines Unternehmens. Die Grenzkostenfunktion der Durchschnittskosten bietet die notwendigen Werkzeuge, um diese Ziele zu erreichen und die Rentabilität zu maximieren.
Ki zukunft der arbeit wie kunstliche intelligenz die arbeitswelt revolutioniert
Marktkauf angebote in ihrer nahe familienfreundlich preiswert einkaufen
Jschlatt wer steckt hinter dem online phanomen
SOLVEDAverage and marginal cost Consider the following cost functions - You're The Only One I've Told
Marginal Product of Labor Formula - You're The Only One I've Told
Chapter 2 Limits and the Derivative - You're The Only One I've Told
marginal average cost function formula - You're The Only One I've Told
marginal average cost function formula - You're The Only One I've Told
Solved Find the marginal average cost function if cost and revenue - You're The Only One I've Told
COST FUNCTION Average and marginal costs - You're The Only One I've Told
How To Calc Marginal Revenue - You're The Only One I've Told
Answered The marginal average cost of producing - You're The Only One I've Told
What Is Marginal Average Cost - You're The Only One I've Told
Cara Menghitung Marginal Cost - You're The Only One I've Told
Solved Suppose that the average cost function is given by - You're The Only One I've Told
How to derive marginal cost How to Calculate Marginal Cost 11 Steps - You're The Only One I've Told
marginal average cost function formula - You're The Only One I've Told
Marginal cost Definition formulas curves and more - You're The Only One I've Told